 Sample Images: Tamron 70-300mm f/4-5.6 Di VC USD SP AF
Sample Images: Tamron 70-300mm f/4-5.6 Di VC USD SP AF Sample Images: Tamron 70-300mm f/4-5.6 Di VC USD SP AF
Sample Images: Tamron 70-300mm f/4-5.6 Di VC USD SP AF(All images copyright Photography Online, Inc.)
Still Life tests, Canon 7D body (sub-frame sensor)
 | |
Still Life tests, Canon 1Ds Mk III body (full-frame sensor)
 | |
VFA Target, Canon 7D body (sub-frame sensor)
 | |
| 70mm f/4 | |
 Upper Left |  Center |
| 70mm f/8 | |
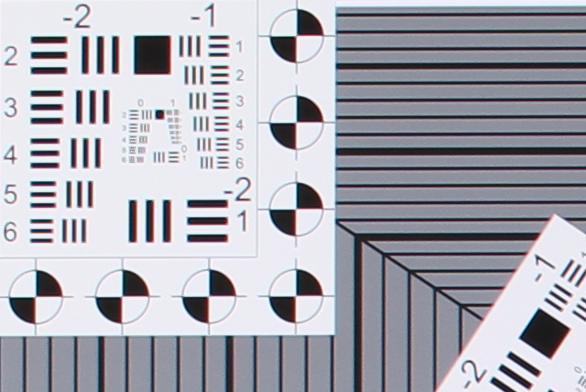 Upper Left |  Center |
| 135mm f/4.5 | |
 Upper Left |  Center |
| 135mm f/8 | |
 Upper Left |  Center |
| 300mm f/5.6 | |
 Upper Left |  Center |
| 300mm f/8 | |
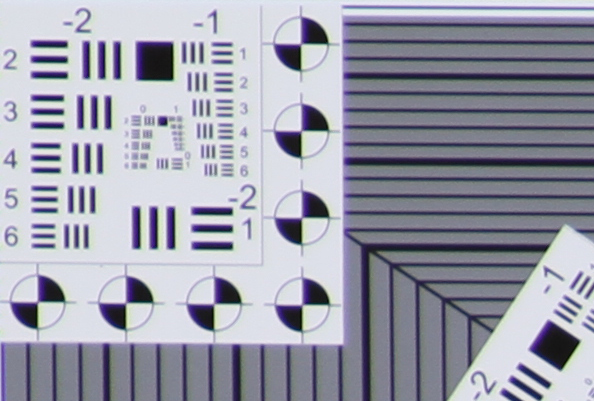 Upper Left |  Center |
VFA Target, Canon 1Ds Mk III body (full-frame sensor)
| 70mm f/4 | |
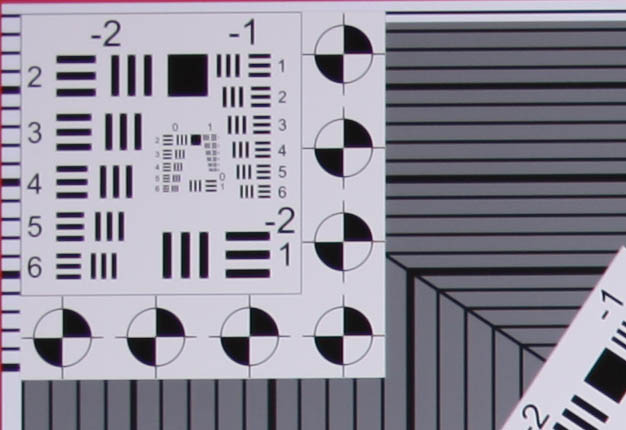 Upper Left |  Center |
| 70mm f/8 | |
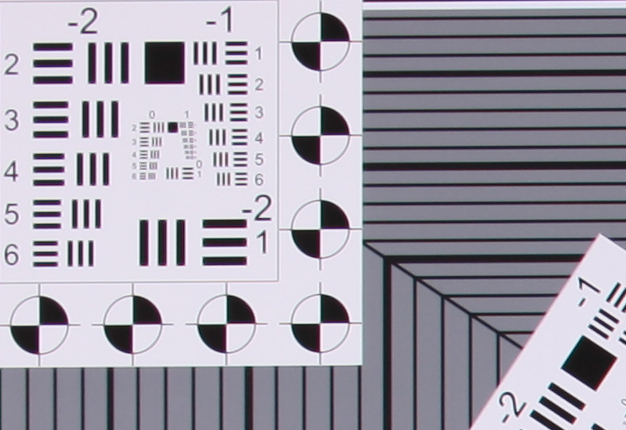 Upper Left |  Center |
| 135mm f/4.5 | |
 Upper Left |  Center |
| 135mm f/8 | |
 Upper Left |  Center |
| 300mm f/5.6 | |
 Upper Left |  Center |
| 300mm f/8 | |
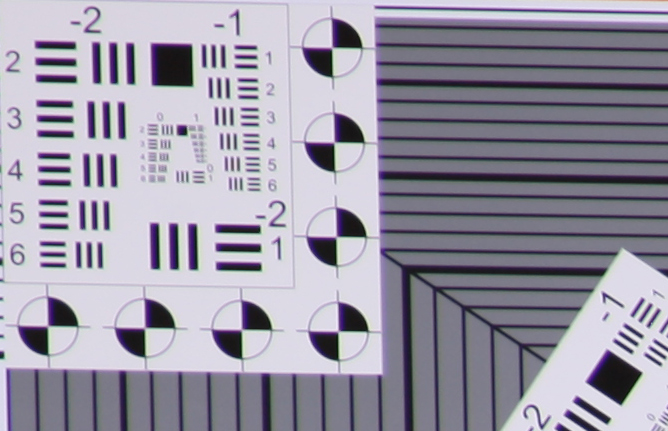 Upper Left |  Center |